Is extending of a TTO experiment to 23 states per respondent justifiable? An empirical answer from Polish EQ-5D valuation study
-
Copyright
© 2013 PRO MEDICINA Foundation, Published by PRO MEDICINA Foundation
User License
The journal provides published content under the terms of the Creative Commons 4.0 Attribution-International Non-Commercial Use (CC BY-NC 4.0) license.
Authors
| Name | Affiliation | |
|---|---|---|
Dominik Golicki |
Department of Experimental and Clinical Pharmacology, Medical University of Warsaw, Poland |
|
Michał Jakubczyk |
Institute of Econometrics, Warsaw School of Economics, PolandDepartment of Pharmacoeconomics, Medical University of Warsaw |
|
Maciej Niewada |
Department of Experimental and Clinical Pharmacology, Medical University of Warsaw, Poland |
|
Witold Wrona |
HealthQuest, Warsaw, Poland |
|
Jan J.V. Busschbach |
Department of Medical Psychology and Psychotherapy, Erasmus University Medical Center, Rotterdam, The Netherlands |
Background: A population of respondents valued 13 EQ-5D health states, using the time trade-off (TTO) method. In further studies, a higher number of states per respondent (16 or 17) was used. Theoretically, with more states per respondent at hand means more available valuations, i.e. higher model estimation accuracy or a possibility to have fewer respondents in a study. A possible problem with extending TTO may be the physical fatigue of respondents who may simply be too tired to credibly answer subsequent questions.
The goal of the study was to evaluate results of TTO experiment expanded to 23 states per respondent in a Polish valuation study.
Methods: A total of 6,769 TTO valuations were available from 305 respondents after exclusions. Regression models were designed, explaining the impact of EQ-5D domains on health state and tested the stability of regression coefficients as more TTO experiments from a single respondent were used. We also performed a statistical and graphical comparison of value sets, made of a varying number of TTO experiments.
Results: Regression coefficients of two parsimonious models, built on 1st-17th (n=5,009) or 18th-23rd (n=1,760) v did not differ significantly in Chow test (p=0.5521). Similarly, regression coefficients of three parsimonious models built on 1st-5th (n=1,461), 6th-17th (n=3,548) or 18th-23rd (n=1,760) valuations, did not differ significantly in the Chow test (p=0.4334), either.
Conclusion: As no systematic changes were found in model parameters, due to TTO experiment extension, no risk of bias or efficiency decrease in model estimation may be assumed. The reported study supports a possibility of more health states per respondent in TTO valuations.
Introduction
Economic analysis is one of the three key components of health technology assessment (HTA) report and cost-utility analysis (CUA) is probably the most common type of economic analysis. In CUA, costs are measured in monetary units and benefits are expressed in quality adjusted life years (QALYs). QALYs are calculated by multiplying the number of life years gained by a quality-of-life weight of a given health state. The methods, which determine quality-of-life weights, are divided into: direct, such as the time-trade off (TTO) method, standard gamble (SG) and visual analogue scale (VAS), or indirect, employing utility instruments, such as EQ-5D, Short Form 6D (SF-6D), Health Utilities Index Mark 2 or Mark 3 (HUI-2 and HUI-3). In order to use a questionnaire as a generic preference tool, somebody has to previously value health states, described by the questionnaire, using one of the above-mentioned direct methods, TTO being the most common in this context. See [1,2] for a detailed description of TTO and the valuation procedure [1,2].
At first, in EQ-5D valuation studies, based on TTO method – in United Kingdom [3], Spain [4], Germany [5] and United States [2] - respondents from the general population valued 13 health states. Some further studies used lower – 7 (Zimbabwe [6]) or extended number of states per respondent - 16 (Denmark [7]) or 17 (Japan [8] and the Netherlands [9]). In a Polish TTO valuation study, 23 health states were presented to each respondent, and this has been the highest number used so far in a general population preference study [10].
Theoretically, a higher number of health states per respondent means more available valuations, what may decrease estimation error and increase estimation model accuracy or allow for fewer respondents in the study; the latter advantage is favorable with regards to obvious budgetary limitations. However, a possible problem with TTO method extension may simply be physical fatigue of respondents to answer the last TTO questions with satisfactory credibility level.
There are different ways to verify if TTO exercise extension results in bias or not. The results of testing the stability of means and variances of consecutive TTO valuations were described in detail elsewhere [10]. Simply, a comparison of health state values, regardless whether assigned in the middle or at the end of experiment, showed no statistically significant differences, neither in means or in variances.
The aim of the present study was to evaluate a possible bias, resulting from TTO experiment expansion to 23 states per respondent in a Polish valuation study. Stability of regression coefficients was assessed in models, based on health state valuations from different stages of TTO experiment.
Materials and methods
Polish valuation study
The data, employed in the reported study, originated from a Polish EQ-5D valuation study, performed in 2008 [10]. That study was based on the modified Measurement and Valuation of Health (MVH) protocol. Each respondent ranked 10 health states, valued four health states, using the VAS methodology and 23, using the TTO method. A total of 7,351 TTO valuations from 321 respondents were available before exclusions and 6,769 from 305 respondents after exclusions (see Table 1).
Table 1. The number of available health state valuations from the Polish EQ-5D TTO-based valuation study after exclusions
| State | Number of valuations as TTO experiment | Total | |||
| 1st-5th | 6th-13th | 14th-17th | 18th-23rd | ||
| 11112 | 66 | 39 | 18 | 33 | 156 |
| 11113 | 28 | 58 | 22 | 41 | 149 |
| 11121 | 61 | 26 | 18 | 32 | 137 |
| 11122 | 54 | 45 | 17 | 42 | 158 |
| 11131 | 33 | 49 | 25 | 33 | 140 |
| 11133 | 22 | 67 | 32 | 42 | 163 |
| 11211 | 54 | 46 | 19 | 35 | 154 |
| 11312 | 32 | 38 | 17 | 48 | 135 |
| 12111 | 66 | 33 | 17 | 17 | 133 |
| 12121 | 53 | 35 | 21 | 26 | 135 |
| 12211 | 46 | 44 | 15 | 25 | 130 |
| 12222 | 42 | 48 | 32 | 35 | 157 |
| 12223 | 14 | 58 | 26 | 33 | 131 |
| 13212 | 32 | 36 | 22 | 44 | 134 |
| 13311 | 25 | 56 | 20 | 31 | 132 |
| 13332 | 19 | 64 | 39 | 40 | 162 |
| 21111 | 55 | 54 | 20 | 27 | 156 |
| 21133 | 22 | 62 | 30 | 48 | 162 |
| 21222 | 37 | 45 | 22 | 33 | 137 |
| 21232 | 26 | 58 | 26 | 50 | 160 |
| 21312 | 31 | 57 | 17 | 46 | 151 |
| 21323 | 16 | 52 | 26 | 39 | 133 |
| 22112 | 52 | 43 | 32 | 29 | 156 |
| 22121 | 51 | 43 | 25 | 21 | 140 |
| 22122 | 50 | 46 | 15 | 44 | 155 |
| 22222 | 71 | 98 | 40 | 81 | 290 |
| 22233 | 11 | 58 | 28 | 45 | 142 |
| 22323 | 27 | 58 | 36 | 37 | 158 |
| 22331 | 18 | 63 | 41 | 40 | 162 |
| 23232 | 26 | 48 | 30 | 37 | 141 |
| 23313 | 20 | 45 | 36 | 40 | 141 |
| 23321 | 16 | 56 | 39 | 49 | 160 |
| 23333 | 33 | 61 | 32 | 35 | 161 |
| 32211 | 22 | 53 | 28 | 29 | 132 |
| 32223 | 21 | 47 | 27 | 46 | 141 |
| 32232 | 22 | 51 | 29 | 60 | 162 |
| 32313 | 23 | 77 | 25 | 38 | 163 |
| 32331 | 23 | 59 | 44 | 35 | 161 |
| 32333 | 27 | 59 | 22 | 43 | 151 |
| 33212 | 13 | 62 | 26 | 38 | 139 |
| 33232 | 17 | 56 | 27 | 42 | 142 |
| 33321 | 15 | 63 | 28 | 34 | 140 |
| 33323 | 27 | 46 | 26 | 43 | 142 |
| 33333 | 42 | 100 | 50 | 93 | 285 |
| Total | 1461 | 2362 | 1187 | 1759 | 6769 |
Study sample, study design, pilot tests, interview procedure, exclusion criteria, modeling and stability of means and variances within TTO experiment tests were described in detail elsewhere [10].
Stability of regression coefficients within TTO experiment
In order to verify the stability of regression coefficients, while using an increasing number of TTO experiments per respondent, the Chow test was employed [11]. The Chow test was performed on the whole sample, divided into two or three subgroups. In the first case, the whole sample was divided into subgroups, with experiments 1-17 (n=5,009) and 18-23 (n=1,760). The second version was designed in such a way as to account for possible instability during the warm-up period in the first TTO experiments. Thus the whole sample was divided into three “periods”: 1-5 (n=1,461), 6-17 (n=3,548) and 18-23 (n=1,760) experiments. In both cases, the basic model with no interaction terms was applied. Accordingly, in the former case, the equality of 11 parameters was tested (constant term and 10 domain specific parameters) in two subperiods and, in the latter one, the equality between the second and the third subperiod was additionally verified (the equivalence of the first and the third subperiod is implied automatically, hence 11 and 22 restrictions, respectively). The null hypothesis was that the parameters are equal in two or three subgroups, as appropriate.
Value sets, based on above-mentioned two or three “period” models, were graphically compared, as well as contrasted with a Polish EQ-5D TTO value set, calculating the following values: (1) the mean absolute difference between health states values, (2) the number of health states (out of 243) with values different by more than 0.01, 0.02, 0.03, 0.05 or 0.10 from the Polish value set and (3) the correlation coefficient between value sets, using simple linear regression.
Results
Regression coefficients of the two parsimonious models, built on valuations from 1-17 or 18-23 experiment, did not differ significantly (p=0.5521; see Table 2).
Table 2. Regression coefficients (SD) of two parsimonious models, built on valuations from 1st-17th or 18th-23rd experiment
| 1st-17th experiment | 18th-23rd experiment | |
| const. | 0.052 (0.021) | 0.039 (0.033) |
| MO2 | 0.047 (0.013) | 0.054 (0.024) |
| MO3 | 0.321 (0.016) | 0.332 (0.03) |
| SC2 | 0.054 (0.014) | 0.059 (0.026) |
| SC3 | 0.233 (0.017) | 0.245 (0.029) |
| UA2 | 0.038 (0.015) | 0.058 (0.03) |
| UA3 | 0.205 (0.016) | 0.237 (0.029) |
| PD2 | 0.049 (0.013) | 0.091 (0.025) |
| PD3 | 0.483 (0.014) | 0.524 (0.025) |
| AD2 | 0.036 (0.014) | -0.002 (0.026) |
| AD3 | 0.227 (0.014) | 0.169 (0.026) |
| Sum of squared errors | 1013.82 | 417.829 |
| The number of observations | 5009 | 1760 |
| Chow test | p=0.5521 |
Similarly, regression coefficients of the three parsimonious models, built on valuations from 1-5, 6-17 or 18-23 experiments, did not differ significantly, either (p=0.4334; see Table 3).
Table 3. Regression coefficients (SD) of three parsimonious models, built on valuations from 1st-5th, 6th-17th 18th-23rd experiment
| 1st-5th experiment | 6th-17th experiment | 18th-23rd experiment | |
| const. | 0.075 (0.024) | 0.029 (0.025) | 0.039 (0.033) |
| MO2 | 0.051 (0.021) | 0.050 (0.016) | 0.054 (0.024) |
| MO3 | 0.331 (0.031) | 0.323 (0.019) | 0.332 (0.03) |
| SC2 | 0.027 (0.021) | 0.061 (0.018) | 0.059 (0.026) |
| SC3 | 0.203 (0.03) | 0.249 (0.021) | 0.245 (0.029) |
| UA2 | 0.016 (0.023) | 0.058 (0.02) | 0.058 (0.03) |
| UA3 | 0.183 (0.028) | 0.218 (0.02) | 0.237 (0.029) |
| PD2 | 0.028 (0.021) | 0.063 (0.017) | 0.091 (0.025) |
| PD3 | 0.447 (0.025) | 0.497 (0.016) | 0.524 (0.025) |
| AD2 | 0.038 (0.022) | 0.031 (0.018) | -0.002 (0.026) |
| AD3 | 0.250 (0.027) | 0.222 (0.016) | 0.169 (0.026) |
| Sum of squared errors | 210.448 | 800.68 | 417.829 |
| The number of observations | 1461 | 3548 | 1760 |
| Chow test | p=0.4334 |
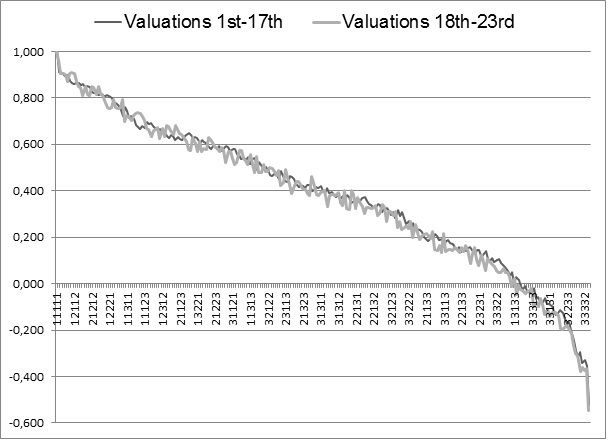
A graphical comparison of the two value sets, based on 1-17 or 18-23 experiments, shows that although individual states differ, both sets are similar (see Figure 1).
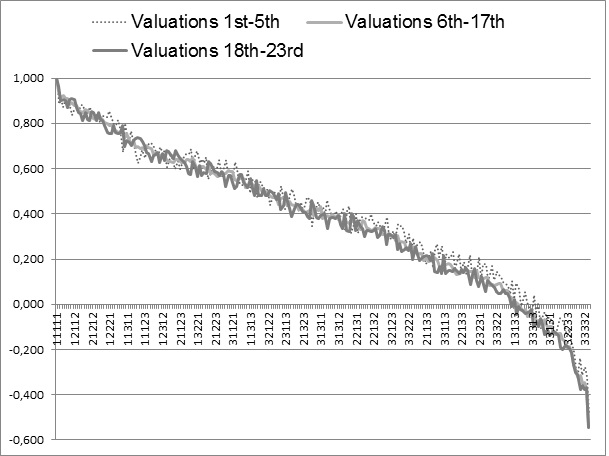
A graphical comparison of three value sets shows that, in a set built on valuations from experiments 1-5 , the health states closest to death are valued somewhat higher than in the two other sets (see Figure 2).
Table 4 presents a statistical summary of cross-model comparisons.
Table 4. Comparison of four different experimental value sets with the Polish EQ-5D TTO value set
| Model built on: | ||||
| valuations from 1st - 5th experiment (n=1,461) | valuations from 6th - 17th experiment (n=3,548) | valuations from 1st-17th experiment (n=5,009) | valuations from 18th-23rd experiment (n=1,760) | |
| Mean absolute difference | 0.031 | 0.009 | 0.009 | 0.022 |
| No. (out of 243) >0.01 vs. Polish | 186 | 83 | 87 | 170 |
| No. (out of 243) >0.02 vs. Polish | 153 | 26 | 13 | 118 |
| No. (out of 243) >0.03 vs. Polish | 120 | 0 | 0 | 70 |
| No. (out of 243) >0.05 vs. Polish | 45 | 0 | 0 | 15 |
| No. (out of 243) >0.10 vs. Polish | 0 | 0 | 0 | 0 |
| R2 vs. Polish TTO value set | 0.990 | 0.999 | 0.999 | 0.994 |
The mean absolute differences between health states values were relatively low (from 0.009 to 0.031) and health states values correlated significantly (R2 from 0.990 to 0.999). The most outlying value set was built on valuations from experiments 1-5.
Discussion
No systematic changes were identified in model parameters after TTO experiment extension. The stability of regression coefficients within TTO experiment was verified using the Chow test and failed to show that parameters were not equal. Value sets, built on experiments 1-5, 6-17, 1-17 or 18-23, were similar, both in cross-comparisons and in a comparison to the Polish EQ-5D value set.
The most outlying value included the valuations from experiments 1-5, what seems fairly normal, as the first TTO valuations are sort of a warm-up task. In valuation of the first health states, respondents learn the rules of and get familiar with TTO exercise. Moreover, the first states differed from the states valued later on, as interviewers were asked not to reveal states worse than death at the beginning of the TTO exercise. The fact that respondents require this warm up period may prompt using more experiments per respondent, so as to outweigh the somewhat atypical initial valuations in subsequent analysis.
The obtained results should be approached together with the earlier presented analysis [10]. Regardless whether the comparison of health state values was assigned in the middle (position 6 to 17) or at the end (position 18 to 23) of the experiment, no statistically significant differences were observed, either in mean values or in variances, using the Holm-Bonferroni correction. We therefore inferred that additional states were valuable by increasing credibility (with identical means) and precision of the final estimation (did not inflate the total variance).
The combined results of both studies have strong practical implications. In a valuation study, an extension of TTO experiment means that more health state valuations will be obtained in the same population of respondents. It also means that credible valuations can be performed in population samples of moderate size. The results may support the estimation of national value sets in other countries, especially in situations of study budget constraints.
Conclusions
The present study supports the use of more health states per respondent in TTO experiments than it was previously assumed. No systematic changes were found in model parameters after TTO experiment extension. Therefore, there is no risk of bias or efficiency decrease in the estimation. This finding provides evidence for the need to improve the efficiency of valuation protocols and supports the estimation of national value sets in other countries.
Acknowledgements
This study was supported in part by unrestricted grants from GSK Commercial, Pfizer Poland, and Astra Zeneca Pharma Poland.
We are grateful to Anna Jabłońska, Anna Jawoszek, Aneta Dwojak, Ola Możeńska, Anna Gąsiewska, Malwina Hołownia, Krzysztof Orłowski, Szymon Zawodnik, Agnieszka Gaczkowska, Adam Golicki, and Łukasz Kołtowski from Student Pharmacoeconomics Chapter, Medical University of Warsaw for assistance in data collection.
Corresponding author
Maciej Niewada, PhD
Department of Experimental and Clinical Pharmacology, Medical University of Warsaw, Poland
Krakowskie Przedmieście 26/28; 00-927 Warsaw, tel. + 22 826 21 16
mail: maciej.niewada@wum.edu.pl or maciej.niewada@gmail.com fax: + 22 8262116
- Dolan P. Modeling valuations for EuroQol health states. Med. Care 1997; 35: 1095–108
- Shaw JW., Johnson JA., Coons SJ. US valuation of the EQ-5D health states: development and testing of the D1 valuation model. Med Care 2005; 43: 203-20
- Dolan P., Gudex C., Kind P., Williams A. The time trade-off method: results from a general population study. Health Econ 1996; 5: 141–54
- Badia X., Roset R., Herdman M., Kind P. A comparison of GB and Spanish general population time trade-off values for EQ-5D health states. Med Decis Making 2001; 21: 7-16
- Greiner W., Claes C., Busschbach JJ., Graf von Schulenburg JM. Validating the EQ-5D with time trade off for the German population. Eur J Health Econ 2005; 6: 124-30
- Jelsma J., Hansen K., De Weerdt W., De Cock P., Kind P. How do Zimbabweans value health states? Popul Health Metr. 2003; 1:11
- Wittrup-Jensen KU., Lauridsen JT., Gudex C., Brooks R., Pedersen KM. Estimating Danish EQ-5D tariffs using TTO and VAS. In: Norinder A., Pedersen K., Roos P., editors. Proceedings of the 18th Plenary Meeting of the EuroQol Group. IHE, The Swedish Institute for Health Economics 2002; 257-292
- Tsuchiya A., Ikeda S., Ikegami N., et al. Estimating an EQ-5D population value set: the case of Japan. Health Econ 2002; 11: 341-53
- Lamers LM., McDonnell J., Stalmeier PF., Krabbe PF., Busschbach JJ. The Dutch tariff: results and arguments for an effective design for national EQ-5D valuation studies. Health Econ 2006; 15: 1121-32
- Golicki D., Jakubczyk M., Niewada M., Wrona W., Busschbach JJ. Valuation of EQ-5D Health States in Poland: First TTO-based Social Value Set in Central and Eastern Europe. Value Health. 2010; 13: 289-97
- Chow GC. Tests of Equality Between Sets of Coefficients in Two Linear Regressions. Econometrica 1960; 28: 591–605